1365. Алгоритм Дейкстры

Задан ориентированный взвешенный граф. Найдите кратчайшее расстояние от вершины s до вершины f.

Вход. В первой строке заданы три числа n, s и f (1 ≤ n ≤ 100, 1 ≤ s, f ≤ n), где n – количество вершин графа. Далее следуют n строк, каждая из которых содержит по n чисел – матрица смежности графа. Число в i-й строке и j-м столбце соответствует ребру, соединяющему вершину i с вершиной j. Если ребра между вершинами нет, то значение равно -1; если ребро существует, то значение представляет собой вес этого ребра. На главной диагонали матрицы всегда стоят нули.

Выход. Выведите искомое кратчайшее расстояние или -1, если пути между вершинами s и f не существует.

Пример входа	Пример выхода
3 1 2 0 -1 2 3 0 -1 -1 4 0	6

РЕШЕНИЕ

графы – алгоритм Дейкстры

Анализ алгоритма

В задаче следует найти кратчайшее расстояние между двумя вершинами в ориентированном взвешенном графе. Для ее решения необходимо реализовать алгоритм Дейкстры.

Пример

Граф, заданный в примере, имеет вид:

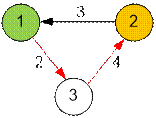
Кратчайшее расстояние от вершины 1 до вершины 2 равно 2 + 4 = 6.

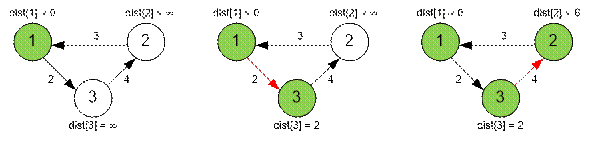
Реализация алгоритма

Объявим используемые константы и массивы.

#define MAX 110

#define INF 0x3F3F3F3F

int m[MAX][MAX], used[MAX], d[MAX];

Читаем входные данные.

scanf("%d %d %d", &n, &s, &f);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++)

{

scanf("%d", &m[i][j]);

if (m[i][j] == -1) m[i][j] = INF;

}

Инициализируем массивы.

memset(used, 0, sizeof(used));

memset(d, 0x3F, sizeof(d));

d[s] = 0;

Запускаем цикл алгоритма Дейкстры. Поскольку граф содержит n вершин, достаточно совершить n – 1 итерацию.

for (i = 1; i < n; i++)

{

Находим вершину с наименьшим значением d[j] среди тех, для которых кратчайшее расстояние от истока еще не вычислено (то есть для которых used[j] = 0). Пусть такой вершиной будет w.

mind = INF;

for (j = 1; j <= n; j++)

if (used[j] == 0 && d[j] < mind) { mind = d[j]; w = j; }

Если невозможно найти вершину для включения в множество вершин, до которых кратчайшее расстояние уже посчитано, завершаем алгоритм.

if (mind == INF) break;

Релаксируем все ребра, исходящие из вершины w.

for (j = 1; j <= n; j++)

if (used[j] == 0) d[j] = min(d[j], d[w] + m[w][j]);

Отмечаем, что кратчайшее расстояние до w уже посчитано (оно находится в d[w]).

used[w] = 1;

}

Выводим ответ – значение d[f]. Если оно равно бесконечности, то пути до вершины f не существует.

if (d[f] == INF) d[f] = -1;

printf("%d\n", d[f]);

Python реализация

Объявим используемые константы.

MAX = 110

INF = float('inf') / 2

Читаем входные данные.

n, s, f = map(int, input().split())

m = [[0] * (n + 1)]

for _ in range(n):

row = list(map(int, input().split()))

m.append([0] + [INF if x == -1 else x for x in row])

Инициализируем списки.

used = [False] * (n + 1)

d = [INF] * (n + 1)

d[s] = 0

Запускаем цикл алгоритма Дейкстры. Поскольку граф содержит n вершин, достаточно совершить n – 1 итерацию.

for _ in range(n - 1):

Находим вершину с наименьшим значением d[j] среди тех, для которых кратчайшее расстояние от истока еще не вычислено (то есть для которых used[j] = 0). Пусть такой вершиной будет w.

mind = INF

w = -1

for j in range(1, n + 1):

if not used[j] and d[j] < mind:

mind = d[j]

w = j

Если невозможно найти вершину для включения в множество вершин, до которых кратчайшее расстояние уже посчитано, завершаем алгоритм.

if mind == INF:

break

Релаксируем все ребра, исходящие из вершины w.

for j in range(1, n + 1):

if not used[j]:

d[j] = min(d[j], d[w] + m[w][j])

Отмечаем, что кратчайшее расстояние до w уже посчитано (оно находится в d[w]).

used[w] = True

Выводим ответ – значение d[f]. Если оно равно бесконечности, то пути до вершины f не существует.

print(-1 if d[f] == INF else d[f])